Учение о возрастании и убывании функций является одной из важнейших тем в курсе математики для учеников 9 класса. Понимание этой темы позволяет ученикам более глубоко вникнуть в мир графиков функций и не только читать, но и анализировать их.
Основная идея заключается в том, что функция называется возрастающей, если с ростом аргумента, значение функции также возрастает. Соответственно, функция убывающей, если с ростом аргумента, значение функции убывает.
Чтобы более наглядно представить, как работает возрастание и убывание функций, рассмотрим примеры. Рассмотрим функцию f(x) = x^2. Можно заметить, что при увеличении аргумента, значение функции также увеличивается. Поэтому данная функция является возрастающей. Также можно рассмотреть функцию g(x) = -x^2. В этом случае, при увеличении аргумента, значение функции уменьшается. Поэтому данная функция является убывающей.
Когда функция возрастает а когда убывает: принципы и примеры
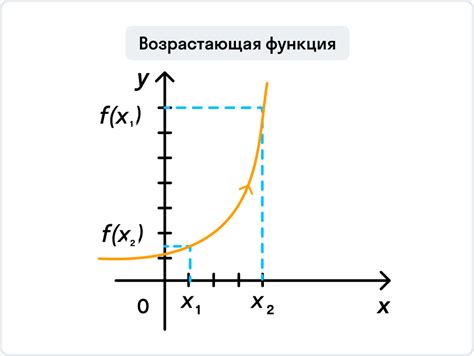
Математические функции могут быть либо возрастающими, либо убывающими, в зависимости от изменения их значений с увеличением аргумента. Этот подход применяется не только в математике, но и в других науках и областях, где требуется анализ данных и понимание тенденций.
Функция называется возрастающей, если ее значения увеличиваются при увеличении аргумента. В противном случае, функция называется убывающей, если ее значения уменьшаются при увеличении аргумента.
Определение возрастания или убывания функции основано на их производных. Если производная функции положительна на определенном интервале, то функция является возрастающей на этом интервале. Если производная функции отрицательна на определенном интервале, то функция является убывающей на этом интервале.
Примеры возрастающих функций:
| Функция | График |
|---|---|
| y = x |  |
| y = e^x |  |
Примеры убывающих функций:
| Функция | График |
|---|---|
| y = -x |  |
| y = -e^x |  |
Понятие возрастания и убывания

Функция называется возрастающей на некотором интервале, если значение функции растет при увеличении аргумента в пределах данного интервала. Иными словами, если смещение аргумента в положительном направлении соответствует смещению функции в положительном направлении, то функция считается возрастающей на данном интервале.
Наоборот, функция называется убывающей на некотором интервале, если значение функции уменьшается при увеличении аргумента в пределах этого интервала. Если смещение аргумента в положительном направлении соответствует смещению функции в отрицательном направлении, то функция считается убывающей на данном интервале.
Знание, как определить выполнение условий возрастания или убывания на заданном интервале, помогает понять поведение функции и делать предположения о ее свойствах без необходимости построения графика.
Например, рассмотрим функцию y = 2x + 3. Коэффициент при аргументе x положительный (2), поэтому при увеличении x значение функции увеличивается. Это означает, что функция возрастает на всей числовой прямой.
Знак производной и возрастание функции
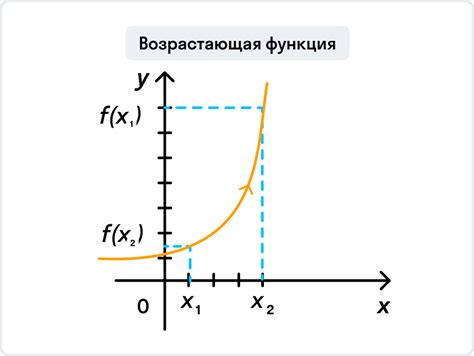
Если производная положительна на каком-то интервале, то функция возрастает на этом интервале. Это значит, что при увеличении значения независимой переменной, значение функции также увеличивается. Например, если производная функции равна 2 на интервале от 0 до 5, то функция возрастает на этом интервале.
Если производная отрицательна на каком-то интервале, то функция убывает на этом интервале. Это значит, что при увеличении значения независимой переменной, значение функции уменьшается. Например, если производная функции равна -3 на интервале от 5 до 10, то функция убывает на этом интервале.
Если же производная равна нулю или не определена в точке, то это может указывать на экстремумы функции – точки максимума или минимума.
Знание знака производной и его интерпретация позволяют нам понять, как функция меняется на разных интервалах и решать различные задачи, связанные с определением экстремумов и интервалов возрастания или убывания функции.
Точки экстремума и монотонности

В математике понятие монотонности описывает поведение функции на промежутке. Функция может быть возрастающей (увеличиваться), убывающей (убывать) или сохранять постоянное значение (быть постоянной).
Точка экстремума - это точка, в которой функция достигает максимального или минимального значения на определенном промежутке. Точка максимума - это точка, в которой функция достигает наибольшего значения, а точка минимума - это точка, в которой функция достигает наименьшего значения.
Для определения монотонности функции и нахождения точек экстремума, можно использовать производные функции. Производная функции дает информацию о ее скорости изменения в каждой точке. Если производная положительна на всем промежутке, то функция возрастает. Если производная отрицательна на всем промежутке, то функция убывает. Точки, в которых производная меняет знак с положительного на отрицательный или наоборот, являются точками экстремума.
Также функция может быть немонотонной, то есть иметь участки возрастания и убывания. На таких участках возможно наличие перегибов - точек, в которых функция меняет свой характер поведения.
| Монотонность | Производная | Точки экстремума | Примеры |
|---|---|---|---|
| Возрастание | Положительная | Минимумы | Функция y = x^2 |
| Убывание | Отрицательная | Максимумы | Функция y = -x^2 |
| Немонотонная | Меняет знак | Перегибы | Функция y = x^3 |
Изучение монотонности и точек экстремума функций позволяет более глубоко понять их свойства и поведение на заданном промежутке.
Примеры возрастающих функций

Функция в математике называется возрастающей, если при увеличении значения аргумента функции, соответствующее значение самой функции также увеличивается.
Вот несколько примеров возрастающих функций:
- Линейная функция: Функция вида y = kx + b, где k и b - коэффициенты, при условии, что k > 0. Например, функция y = 2x + 1 является возрастающей, так как при увеличении x на 1, значение функции увеличивается на 2.
- Показательная функция: Функция вида y = a^x, где a > 1. Например, функция y = 2^x является возрастающей, так как при увеличении x на 1, значение функции увеличивается вдвое.
- Тригонометрическая функция: Некоторые тригонометрические функции, такие как y = sin(x) и y = cos(x), также являются возрастающими на некоторых интервалах.
Знание того, когда функция возрастает, является важным для анализа графика функции и решения математических задач. Помните, что для возрастающих функций изменение аргумента влечет за собой увеличение значения функции.
Примеры убывающих функций

- Линейная функция: y = -2x + 4. При увеличении x на единицу, значение y уменьшается на 2.
- Квадратичная функция: y = -x2 + 3x - 1. При увеличении x на единицу, значение y уменьшается.
- Экспоненциальная функция: y = 2-x. При увеличении x на единицу, значение y уменьшается.
- Логарифмическая функция: y = log2 x. При увеличении x на единицу, значение y уменьшается, так как логарифм убывает.
Это лишь несколько примеров убывающих функций. Всего существует множество различных математических функций, значения которых уменьшаются по мере изменения аргумента.
Например, зная, что функция возрастает на определенном интервале, мы можем использовать это знание, чтобы оптимизировать процессы. Например, в экономике, зная функцию, описывающую зависимость продаж от цены, мы можем найти оптимальную цену, при которой мы получим максимальную прибыль.
Кроме того, знание о возрастании и убывании функции может быть полезным при решении геометрических задач. Например, зная, что функция убывает на определенном интервале, мы можем доказать, что две прямые линии никогда не пересекутся, и использовать эту информацию при построении графиков и решении задач связанных с геометрией.
Таким образом, понимание того, когда функция возрастает и когда убывает, является ключевым навыком, который помогает не только в предмете математика, но и в реальной жизни. Этот навык позволяет нам лучше понять мир вокруг нас и использовать это понимание для решения различных задач.



