Тригонометрические функции, в частности синус и косинус, являются одними из самых важных понятий в математике. Они позволяют устанавливать зависимости между углом и отношениями сторон в треугольнике. Однако, при некоторых значениях угла, значение синуса равно нулю, что влечет за собой определенные особенности в поведении тригонометрических функций.
Когда синус равен нулю, это означает, что соответствующий угол находится в одном из следующих положений: 0°, 180°, 360° и так далее. В этих положениях синус равен нулю, тогда как косинус принимает значение 1. Другими словами, при данных значениях угла, противоположная сторона треугольника имеет нулевую длину, а прилежащая сторона имеет длину, равную гипотенузе.
При использовании в тригонометрических функциях соответствующих углов, когда синус равен нулю, возникает равенство sin(0°) = sin(180°) = sin(360°) = 0. Это свойство синуса может использоваться для решения различных задач в физике, геометрии и других науках. Например, при изучении колебаний, углы, кратные 180°, могут иметь значимое значение, так как в этих моментах колеблющаяся система находится в начальном или конечном положении.
Особенности тригонометрических функций при синусе, равном нулю
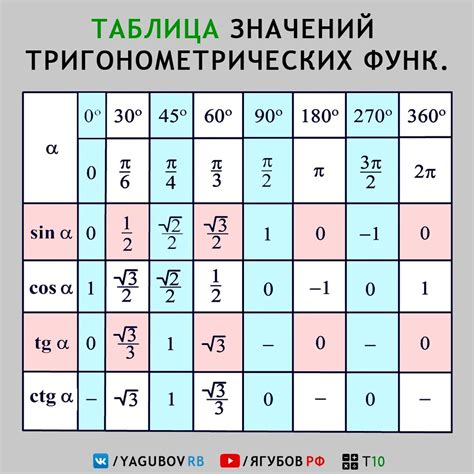
Когда синус равен нулю, это означает, что противоположная сторона треугольника равна нулю, то есть треугольник становится вырожденным. В результате этого происходят несколько интересных особенностей, связанных с другими тригонометрическими функциями.
- Косинус – это тригонометрическая функция, которая также представляет отношение сторон треугольника. Когда синус равен нулю, косинус принимает значение 1 или -1, в зависимости от положения угла.
- Тангенс – это отношение противоположной стороны к прилежащей стороне треугольника. При синусе, равном нулю, тангенс становится неопределенным, поскольку сторона, на которую делится противоположная сторона, также равна нулю.
- Котангенс – это обратное значение тангенса. При синусе, равном нулю, котангенс также становится неопределенным.
Таким образом, при синусе, равном нулю, косинус принимает фиксированное значение, а тангенс и котангенс становятся неопределенными. Эти особенности могут использоваться при решении математических и физических задач, а также при изучении свойств треугольников и тригонометрических функций.
Асимптотическое поведение

Графически это выглядит следующим образом:
| Аргумент | Косинус |
|---|---|
| 0.1 | 0.995004 |
| 0.01 | 0.999950 |
| 0.001 | 0.999995 |
| 0.0001 | 0.999999 |
Из этой таблицы видно, что с уменьшением значения аргумента, значение косинуса стремится к 1. Это явление точно выражено в математической формулировке асимптотического поведения косинуса. Оно может быть полезно при решении различных задач, например, при нахождении пределов функций или при аппроксимации значений.
Периодические свойства
Период функции синус равен π или приближенно 3,14, что означает, что синус повторяется каждые 3,14 радиан или 180 градусов. Это связано с тем, что синус принимает значение 0 каждый раз, когда его аргумент равен nπ, где n - любое целое число.
Аналогичным образом, косинус также является периодической функцией с периодом π. Он также принимает значение 0 каждый раз, когда его аргумент равен (n+0.5)π.
Периодичность тригонометрических функций синус и косинус имеет множество практических применений, включая моделирование колебаний, анализ звуковых волн, изучение электрических и механических колебаний и многое другое.
Изменение знака

Когда синус равен нулю, это означает, что аргумент функции находится в точках, где значения синуса меняют свой знак. Такие точки называются нулями синуса.
Нули синуса лежат на оси абсцисс в точках, где аргумент функции равен целому числу умноженному на π: x = kπ, где k - целое число. Это является следствием периодичности синуса, так как sin(x) = sin(x + 2π).
Таким образом, значения синуса меняют свой знак при прохождении через каждый ноль. Нули синуса можно наглядно представить на графике с помощью пересечений графика с осью абсцисс.
Особенность изменения знака синуса также распространяется и на другие тригонометрические функции, такие как косинус и тангенс. При прохождении через ноль, значения этих функций также меняют свой знак.
Взаимосвязь с другими функциями

Косинус и синус образуют две взаимно-обратные функции, то есть sin(90° - x) = cos(x) и cos(90° - x) = sin(x). Это соотношение позволяет легко перейти от синусной функции к косинусной и наоборот.
Кроме того, синус и косинус связаны с тангенсом следующим образом: tan(x) = sin(x) / cos(x). Это равенство позволяет выразить тангенс через синус и косинус. Также можно использовать тригонометрические тождества для выражения синуса и косинуса через тангенс и наоборот.



