</p>
Математические модели являются одной из ключевых составляющих математического анализа и исследования. Они представляют собой упрощенное и формализованное описание реальных явлений и процессов с использованием математических методов и концепций. Применение математических моделей позволяет улучшить понимание сложных систем, предсказывать их поведение, принимать обоснованные решения и проводить различные исследования.
Основные принципы построения математических моделей включают формулирование задачи, выбор математической структуры, определение параметров и условий, а также проверку и анализ результатов. Как правило, математические модели строятся на основе математических уравнений, функций, графов, вероятностных распределений и других математических концепций.
Примерами математических моделей могут служить модель распространения эпидемии, модель динамики популяции, модель финансового рынка, модель движения тела и другие. Эти модели представляют собой абстрактное отображение реальной ситуации, которое позволяет проводить различные эксперименты, прогнозировать результаты и изучать особенности и закономерности рассматриваемых процессов.
Как правило, математические модели требуют математических навыков и знаний, чтобы быть эффективно построены и использованы. Они широко применяются в научных исследованиях, инженерных задачах, экономическом анализе, финансовых прогнозах, оптимизации процессов и многих других областях. Важно отметить, что математическая модель всегда является упрощением реальной ситуации, поэтому важно корректно выбирать и использовать модель в зависимости от поставленных целей и требований.
Математические модели: определение и назначение

Математическая модель - абстрактное представление реального объекта, процесса или системы с использованием математических символов, уравнений и операций. Она представляет собой формализацию и упрощение реальности, позволяющую анализировать и предсказывать поведение объектов или явлений.
Основной целью создания математических моделей является получение количественного описания и понимания сложных систем, которые не могут быть полностью охарактеризованы или изучены с помощью экспериментов или наблюдений. Математические модели позволяют упростить систему до набора уравнений и правил, которые описывают ее ключевые характеристики и динамику.
Применение математических моделей широко распространено в различных областях науки и техники. В физике, например, модели используются для описания движения тел, прогнозирования погоды или прогнозирования поведения сложных систем, таких как галактики. В экономике и финансах модели помогают прогнозировать тенденции и поведение рынков, а также оценивать риски. В медицине математические модели применяются для изучения распространения заболеваний и оптимизации лечения.
Существует несколько типов математических моделей. Дискретные модели описывают системы, где состояние может изменяться только в конкретные моменты времени (например, модель эволюции популяции). Непрерывные модели используются для описания систем, где состояние может изменяться в любой момент времени и представляется как непрерывная функция (например, модель движения тела по законам физики).
Важно отметить, что математическая модель - это упрощенное отражение реальности, и она может быть ограничена в своей применимости. Некоторые аспекты системы могут быть упущены или упрощены, что может влиять на точность прогнозов и результаты анализа. Поэтому создание и использование математических моделей требует осторожного подхода и проверки на соответствие с реальностью.
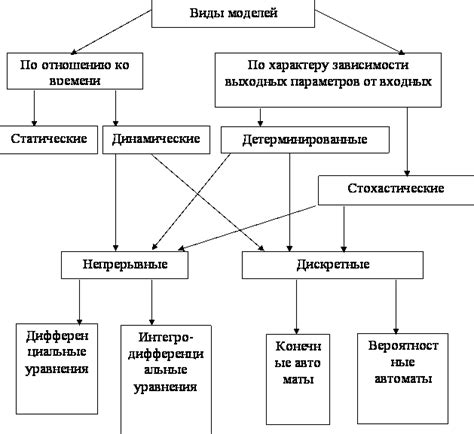
Виды математических моделей
Математическое моделирование используется во многих областях науки, техники, экономики и других сферах деятельности. В зависимости от целей моделирования и конкретной области применения существуют различные виды математических моделей.
- Аналитические модели - это модели, которые основываются на математических уравнениях и формулах. Они позволяют получить точное аналитическое решение и дать строгое математическое обоснование. Примерами аналитических моделей могут быть модели физических процессов, таких как движение тела в поле силы, или экономические модели, описывающие зависимость спроса и предложения от цены товара.
- Эмпирические модели - это модели, основанные на экспериментальных данных и наблюдениях. Они используются в тех случаях, когда точные математические уравнения или формулы неизвестны или сложно получить. Вместо этого эмпирические модели используют статистические методы и анализ данных. Примерами эмпирических моделей могут быть модели прогнозирования погоды или модели экономического роста на основе статистических данных о прошлом.
- Симуляционные модели - это модели, в которых процесс моделирования основан на имитации реальной системы или процесса. Они используются для изучения сложных систем, где неизвестны точные математические законы. Вместо этого симуляционные модели включают в себя набор правил или алгоритмов, которые позволяют имитировать поведение системы во времени. Примерами симуляционных моделей могут быть модели развития городов или модели производственных процессов в промышленности.
- Графические модели - это модели, в которых используется графическое представление для описания объектов и связей между ними. Графические модели часто используются в компьютерной графике, компьютерном зрении и компьютерном моделировании. Они позволяют визуализировать сложные системы и процессы, что облегчает их анализ и понимание. Примерами графических моделей могут быть модели трехмерных объектов или схемы сетей связи.
Каждый из перечисленных видов математических моделей имеет свои особенности и применяется в зависимости от задачи моделирования и доступных данных. Выбор подходящей модели является важным шагом для достижения точных результатов и понимания исследуемого процесса или системы.
Принципы построения математических моделей

1. Формализация
Одним из основных принципов построения математических моделей является процесс формализации, то есть перевод нечёткой и наблюдаемой действительности в чёткие математические термины и символы. Формализация позволяет точно определить, какие факторы будут учтены в модели, и как они будут взаимодействовать.
2. Упрощение
При построении математической модели необходимо упрощать реальность, исключая некоторые сложные факторы и аспекты. Упрощение позволяет сделать модель более понятной и удобной для анализа, несмотря на потерю некоторой точности.
3. Детерминированность
Математические модели могут быть детерминированными, то есть строиться на основе точных математических законов и уравнений, либо вероятностными, основанными на статистических данных и вероятностных распределениях. Детерминированность позволяет получить точное представление о системе и ее поведении.
4. Проверка и адаптация
После построения математической модели необходимо провести её проверку на соответствие реальным данным и провести адаптацию модели, если это требуется. Этот процесс включает в себя сравнение результатов моделирования с экспериментальными данными и внесение необходимых корректировок для улучшения совпадения модели и наблюдаемой действительности.
5. Валидация
После проверки и адаптации математической модели необходимо провести валидацию – проверить, насколько точно модель предсказывает поведение системы вне известного диапазона данных. Валидация позволяет убедиться в достоверности результатов моделирования и использовать их для прогнозирования и принятия решений.
6. Итерационность
Итерационность является важным принципом построения математических моделей, так как модель может быть усовершенствована и изменена в процессе её использования и дальнейшего анализа. Итерационный процесс позволяет постепенно совершенствовать модель и учеть все новые исследования и результаты экспериментов.
Детерминированные математические модели
Детерминированные математические модели - это модели, которые основаны на точных математических уравнениях и правилах. Они предназначены для предсказания поведения системы на основе известных начальных условий и параметров модели. Детерминированные модели используются в различных областях, включая физику, экономику, биологию, социальные науки и др.
Принципы детерминированных математических моделей:
- Формулирование проблемы: определение целей моделирования, постановка задачи и определение переменных и параметров модели.
- Построение математической модели: разработка математических уравнений, связывающих переменные и параметры модели.
- Решение математической модели: применение методов решения уравнений модели для получения решения и предсказания поведения системы.
- Валидация и верификация модели: проверка правильности модели и ее соответствия реальной системе.
- Интерпретация результатов: анализ полученных результатов, их интерпретация и выводы для дальнейшего принятия решений.
Примеры детерминированных математических моделей:
- Модель движения тела под действием силы тяжести. Эта модель описывает движение тела в свободном падении или бросок тела под углом.
- Модель роста популяции. Эта модель описывает изменение численности популяции с течением времени с учетом рождаемости, смертности и миграции.
- Модель экономического роста. Эта модель описывает изменение уровня производства и экономического развития в зависимости от инвестиций, технологического прогресса и других факторов.
Детерминированные математические модели являются важным инструментом предсказания поведения системы и принятия решений на основе точных математических законов и уравнений.
Примеры детерминированных математических моделей
Детерминированные математические модели представляют систему в виде точных математических уравнений, которые описывают зависимости между различными переменными. Вот несколько примеров таких моделей:
Модель экспоненциального роста
Эта модель описывает процесс экспоненциального роста количества некоторого ресурса или популяции. Уравнение, описывающее эту модель, имеет вид:
Y(t) = Y(0) * e^(k*t)
где Y(t) - количество ресурса или популяции в момент времени t, Y(0) - начальное количество ресурса или популяции, k - коэффициент роста, e - основание натурального логарифма.
Модель движения тела под действием силы
Эта модель описывает движение тела под действием силы, например, гравитации. Уравнение, описывающее эту модель, называется уравнением Ньютона:
F = m * a
где F - сила, действующая на тело, m - масса тела, a - ускорение тела.
Модель распространения инфекции
Эта модель описывает распространение инфекции в популяции. Уравнение, описывающее эту модель, может иметь вид:
dI/dt = β * I * (N - I) / N
где dI/dt - скорость изменения количества зараженных, β - коэффициент заражаемости, I - количество зараженных, N - общее население.
Это лишь некоторые примеры детерминированных математических моделей, их существует гораздо больше. Они позволяют более точно и предсказуемо анализировать и описывать различные системы и процессы в науке, инженерии и других областях.
Вероятностные математические модели
Вероятностная математическая модель - это математическая модель, которая основана на понятии вероятности. Она используется для описания случайных явлений и предсказания их возможных результатов.
Основные принципы вероятностной математической модели:
- Вероятностное пространство: это множество всех возможных результатов случайного явления. Каждый результат называется элементарным исходом. Вероятностное пространство обозначается символом Ω.
- События: это подмножества вероятностного пространства. Событие происходит, если реализуется какой-то элементарный исход.
- Вероятность: это числовая характеристика события, которая показывает, насколько вероятно выпадение такого события.
Примеры вероятностных математических моделей:
- Модель Бернулли: это модель, которая описывает случайный эксперимент с двумя возможными исходами: «успех» и «неудача». Вероятность успеха обозначается p, а вероятность неудачи - q = 1 - p.
- Модель Биномиальное распределение: это модель, которая описывает случайный эксперимент, состоящий из n независимых испытаний по модели Бернулли. Распределение вероятностей описывается биномиальным коэффициентом.
- Модель Пуассоновского распределения: это модель, которая описывает число появления событий в фиксированном промежутке времени или пространстве.
Примеры вероятностных математических моделей

Вероятностные математические модели находят применение во многих областях, таких как экономика, финансы, наука о данных и технологии, биология, и т.д. Ниже приведены некоторые известные примеры вероятностных математических моделей:
Модель Маркова:
Модель Маркова представляет собой математическую модель, которая описывает последовательность событий, где вероятность будущего события зависит только от текущего состояния системы. Эта модель находит применение во многих областях, таких как финансовые рынки, моделирование климата, генетика и т.д.
Модель Бернулли:
Модель Бернулли используется для моделирования случайных экспериментов с двумя исходами - успехом и неудачей. Вероятность успеха и неудачи остается постоянной при каждом испытании. Эта модель находит применение во многих областях, таких как статистика, теория игр, исследование операций и т.д.
Модель Пуассона:
Модель Пуассона используется для моделирования событий, которые происходят в случайные моменты времени без определенного порядка. Эта модель находит применение в областях, где важно предсказывать количество событий в заданном интервале времени, таких как телекоммуникации, интернет-трафик, финансовые рынки и т.д.
Модель Ляпунова:
Модель Ляпунова используется для исследования стабильности и устойчивости динамических систем. Эта модель находит применение в теории управления, физике, экономике и других областях, где важно понимать, какие значения параметров приведут к устойчивому состоянию системы.
Модель Гаусса:
Модель Гаусса, или нормальное распределение, используется для моделирования случайных величин, которые подчиняются нормальному распределению. Эта модель находит широкое применение в статистике, физике, финансах, экономике и других областях, где важно оценивать вероятность различных значений случайной величины.
Дискретные математические модели
Дискретные математические модели являются одним из основных инструментов математического моделирования. Они позволяют описывать и анализировать процессы, которые происходят в дискретных системах, то есть системах, где состояние меняется только в определенные моменты времени.
Дискретные математические модели находят применение в различных областях, таких как информационные технологии, логистика, экономика, теория вероятностей и другие. Они позволяют решать разнообразные задачи: от оптимизации производственных процессов до прогнозирования поведения системы.
Одной из основных концепций дискретных математических моделей является понятие состояния. Состояние может быть описано с помощью дискретных переменных, которые могут принимать определенные значения из заданного множества. Кроме того, важную роль играют переходы между состояниями, которые определяются правилами модели.
Примером дискретной математической модели является модель марковского процесса. В этой модели состояние системы меняется в дискретные моменты времени в соответствии с заданными вероятностями переходов. Марковские модели часто используются для моделирования случайных процессов, например, для описания поведения финансовых рынков или прогнозирования климатических изменений.
Другим примером дискретной математической модели является модель сети. В этой модели элементы системы представлены вершинами графа, а связи между элементами - ребрами. Моделирование с использованием сетей позволяет анализировать процессы, происходящие в сложных системах, таких как транспортные или коммуникационные сети.
Дискретные математические модели являются мощным инструментом для анализа и оптимизации различных систем. Они позволяют предсказывать поведение системы, оценивать эффективность различных стратегий и принимать обоснованные решения на основе математической модели.
Примеры дискретных математических моделей
Дискретная математика занимается изучением объектов, которые имеют конечный или счетный набор значений. В этой области математики разрабатываются различные модели, которые представляют дискретные системы и процессы. Вот несколько примеров дискретных математических моделей:
Графы: графы являются одним из основных объектов изучения дискретной математики. Граф представляет собой совокупность вершин, соединенных ребрами. Графы используются для представления связей между объектами, таких как дорожные сети, сети передачи данных, социальные сети и т.д. Графы могут быть направленными или ненаправленными, взвешенными или невзвешенными.
Теория вероятностей: теория вероятностей рассматривает случайные явления. В дискретной математике теория вероятностей используется для моделирования случайных процессов с конечным или счетным множеством исходов. Например, можно моделировать результат броска монеты или броска кубика с помощью вероятностных моделей.
Теория чисел: теория чисел изучает свойства целых чисел. В дискретной математике теория чисел используется для изучения различных алгоритмов шифрования, факторизации чисел, генерации случайных чисел и других задач, связанных с целыми числами.
Комбинаторика: комбинаторика изучает счетные множества и вопросы их комбинаторного анализа. Комбинаторика используется для решения задач, связанных с подсчетом и размещением объектов, определением вероятности сочетаний и перестановок, анализа структуры объектов и других задач.
Теория игр: теория игр изучает модели стратегического поведения в конфликтных ситуациях. В дискретной математике теория игр используется для анализа игры с нулевой суммой, нахождения равновесия Нэша и разработки стратегий для игры.
Это лишь несколько примеров дискретных математических моделей, которые используются для анализа и представления различных дискретных систем и процессов. Дискретная математика играет важную роль во многих областях науки и техники, таких как компьютерные науки, теория информации, криптография, сетевые технологии, искусственный интеллект и другие.
Континуальные математические модели
Континуальные математические модели являются одним из основных направлений в математическом моделировании и используются для описания явлений и процессов в непрерывном пространстве или времени.
Основной принцип континуальных моделей заключается в представлении системы как непрерывного математического объекта, который описывается дифференциальными уравнениями или интегральными уравнениями.
Примерами континуальных математических моделей являются:
- Уравнение Навье-Стокса – используется для описания движения жидкостей и газов;
- Уравнение теплопроводности – описывает распределение температуры в твердых телах;
- Уравнение диффузии – описывает распределение концентрации вещества в пространстве;
- Уравнение колебаний – используется для описания механических колебаний;
- Уравнение волнового типа – описывает распространение волн в различных средах.
Для решения континуальных математических моделей применяются различные методы, включая численные методы, аналитические методы и методы приближения.
Континуальные математические модели являются важным инструментом для изучения и предсказания различных процессов, как в естественных, так и в технических науках, и широко применяются в физике, химии, биологии, экономике и других областях знания.
Вопрос-ответ
Какие принципы лежат в основе математических моделей?
Основным принципом математических моделей является использование математических методов и инструментов для описания и анализа различных явлений и процессов в реальном мире. Математические модели стремятся упростить сложные системы и отношения между ними, чтобы сделать возможным их изучение и прогнозирование.
Какие примеры математических моделей существуют?
Примерами математических моделей могут служить модели экономических процессов, модели погоды и климата, модели движения тел, модели распространения инфекционных заболеваний и многие другие. Например, модель экономического рынка может использовать математические уравнения для описания спроса и предложения товаров, а модель погоды - для прогнозирования температуры, давления и других показателей.
Какой общий подход к построению математической модели?
Построение математической модели обычно включает несколько шагов. Вначале необходимо определить цель исследования или прогнозирования и явления, которые будут моделироваться. Затем следует выбрать математические методы и инструменты, которые будут использоваться для описания и анализа этих явлений. После этого производится построение самой модели, которая включает в себя уравнения, параметры и начальные условия. Наконец, модель тестируется и применяется для получения результатов и прогнозов.
Какие типы математических моделей можно выделить?
Существует несколько типов математических моделей. Это статические модели, которые описывают состояние системы в конкретный момент времени или в определенных условиях, и динамические модели, которые учитывают изменение состояния системы во времени. Также можно выделить детерминистические модели, которые предсказывают конкретные результаты, и стохастические модели, которые учитывают случайность и вероятности. Кроме того, есть модели с дискретным временем и модели с непрерывным временем.