Системы исчисления являются основой для представления чисел в различных сферах научных и практических исследований. Они позволяют нам декодировать информацию и проводить математические операции. Существует несколько видов систем исчисления, которые используют разные основания и символы для представления чисел.
Одной из наиболее распространенных систем исчисления является десятичная система, которая использует 10 символов (цифры от 0 до 9) и основание 10. Однако, помимо десятичной системы, существуют и другие системы исчисления, такие как двоичная, восьмеричная и шестнадцатеричная.
В двоичной системе исчисления используются всего два символа - 0 и 1. Она широко применяется в электронике и компьютерных науках, так как компьютеры работают с двоичными данными. Восьмеричная система использует 8 символов (цифры от 0 до 7) и основание 8. Ее часто используют в программировании и операционных системах.
Шестнадцатеричная система исчисления использует 16 символов: цифры от 0 до 9 и буквы от A до F. Она широко применяется в программировании, особенно при работе с памятью и цветами. Шестнадцатеричная система позволяет упростить работу с большими числами и улучшает читаемость кода.
Десятичная система исчисления

Десятичная система исчисления, также известная как десятичная система, является наиболее распространенным способом представления чисел. Она основана на основании 10 и использует десять цифр - от 0 до 9 - для обозначения чисел.
В десятичной системе каждая позиция числа имеет вес, определенный его положением относительно запятой. Целая часть числа располагается слева от запятой, а десятичная часть - справа.
Например, число 123,45 в десятичной системе разбивается на:
- 1 - цифра с весом 100 (10^2)
- 2 - цифра с весом 10 (10^1)
- 3 - цифра с весом 1 (10^0)
- 4 - цифра с весом 0,1 (10^-1)
- 5 - цифра с весом 0,01 (10^-2)
Десятичная система исчисления широко используется в повседневной жизни, в торговле, финансах и науке. Она является основой для многих других систем исчисления, таких как двоичная, восьмеричная и шестнадцатеричная.
Двоичная система исчисления
Двоичная система исчисления (также называемая бинарной системой) является одной из основных систем исчисления. В отличие от десятичной системы исчисления, которую мы обычно используем в повседневной жизни, двоичная система основана на двух цифрах: 0 и 1.
В двоичной системе каждая позиция числа имеет вес, который является степенью числа 2. Например, в двоичной системе число 1010 представляет собой сумму 1x2^3 + 0x2^2 + 1x2^1 + 0x2^0 = 8 + 0 + 2 + 0 = 10.
Использование двоичной системы исчисления широко распространено в компьютерной технике. Все данные в компьютере представлены в виде двоичных чисел, а каждый бит (бинарная цифра) является основным элементом информации. Набор совокупных битов образуют байты, которые используются для хранения и обработки данных.
Помимо использования в компьютерах, двоичная система исчисления имеет широкий диапазон применений в других областях. Например:
- Телекоммуникации: двоичные коды используются для передачи информации по каналам связи.
- Логика: двоичные числа используются для представления логических состояний, например «истина» и «ложь».
- Математика: двоичная система исчисления является основой для работы с битами и байтами, что позволяет выполнять различные операции, такие как сложение, умножение и др.
Таким образом, двоичная система исчисления играет важную роль в современном мире, особенно в контексте компьютерных технологий и телекоммуникаций. Понимание основных принципов данной системы позволяет лучше понять работу компьютеров и других устройств, а также использовать двоичные числа в различных математических и логических операциях.
Восьмеричная система исчисления

Восьмеричная система исчисления, также известная как октальная система, является позиционной системой счисления, в которой основание равно 8. В этой системе используются восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7.
Восьмеричная система исчисления имеет свои особенности, которые отличают ее от других систем:
- Основание 8 означает, что каждая позиция числа в восьмеричной системе представляет собой степень 8.
- Цифры 0-7 используются для представления значений в каждой позиции числа.
- Чтобы представить числа больше 7, нужно использовать дополнительные позиции числа.
- Восьмеричная система удобна для представления двоичных чисел, так как каждая цифра восьмеричной системы соответствует блоку из трех двоичных цифр.
Преобразование чисел из десятичной системы в восьмеричную и наоборот осуществляется путем деления и умножения на основание системы (8). Для перевода числа восьмеричной системы в десятичную необходимо разложить число по разрядам и перемножить каждый разряд на 8 в степени соответствующего порядка. Для обратного перехода следует разложить число десятичной системы по разрядам и найти остатки от деления на 8, чтобы получить цифры восьмеричной системы.
Восьмеричная система исчисления используется в различных областях, например:
- В программировании для представления битовых сигналов и двоичных чисел.
- В компьютерных сетях для адресации сетевых устройств.
- В электронике для представления восьмибитных данных.
Знание и понимание восьмеричной системы исчисления является важным для программистов и специалистов в области компьютерных наук.
Шестнадцатеричная система исчисления
Шестнадцатеричная система исчисления, также известная как система счисления по основанию 16, является одной из самых распространенных систем исчисления в информатике и программировании. В шестнадцатеричной системе используются шестнадцать цифр, обозначаемых символами от 0 до 9 и от A до F. Всего в системе шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Шестнадцатеричные числа записываются так же, как и числа в десятичной системе с тем отличием, что могут содержать латинские буквы.
Шестнадцатеричная система исчисления широко используется в программировании для представления чисел, адресов памяти и цветов. В компьютерных системах каждый байт, или 8 бит, может быть представлен двумя шестнадцатеричными символами, что облегчает чтение и запись двоичного кода, используемого компьютерами.
При работе с шестнадцатеричными числами важно учитывать, что символы A, B, C, D, E и F имеют значения 10, 11, 12, 13, 14 и 15 соответственно. Таким образом, число "1A" в шестнадцатеричной системе эквивалентно числу "26" в десятичной системе.
Шестнадцатеричные числа могут записываться как целые числа, так и числа с плавающей точкой. Кроме того, они могут быть представлены в виде чисел с префиксами, которые указывают на систему счисления. Например, префикс "0x" используется для обозначения шестнадцатеричных чисел в языке программирования C и многих других.
Шестнадцатеричная система исчисления является удобной и компактной формой представления чисел, особенно в контексте информатики и программирования. Она позволяет эффективно работать с двоичным кодом и представлять большие числа с помощью относительно небольшого количества символов.
Система исчисления восемью
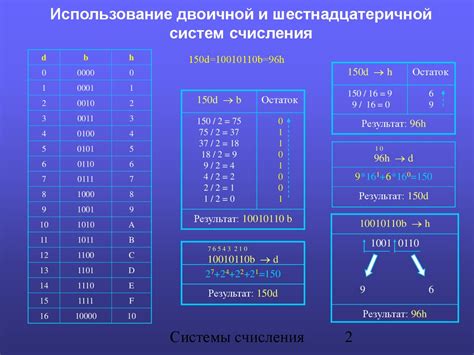
Система исчисления восемью, или октальная система, это позиционная система счисления, в которой основание системы равно 8. То есть, в этой системе используются числа от 0 до 7.
Октальная система широко применяется в компьютерных системах, так как каждый символ в компьютере представляется в виде битовой последовательности длиной в 8 битов, или 1 октет. Каждый бит может принимать одно из двух значений: 0 или 1. Использование октальной системы позволяет легко представлять эти октеты в удобной для чтения форме.
В октальной системе каждая позиция числа имеет свою степень основания 8. Например, число 123 в октальной системе представляет собой: 1 * 8^2 + 2 * 8^1 + 3 * 8^0 = 83 в десятичной системе.
Октальная система использует цифры от 0 до 7 для представления чисел. Таким образом, каждая цифра в октальной системе может быть представлена с помощью 3-х двоичных цифр. Например, цифра 2 в октальной системе равна 010 в двоичной системе.
В октальной системе числа записываются так же, как в десятичной, но используя только цифры от 0 до 7. Например: 10, 20, 30, 40 и так далее.
Октальная система представляет собой удобный способ представления и обработки данных в компьютерных системах, особенно в низкоуровневом программировании.
Применение систем исчисления в компьютерных науках
Системы исчисления являются важной частью различных компьютерных наук, таких как компьютерная архитектура, алгоритмы, программирование и криптография. Они используются для представления и манипулирования данных и информации.
Одним из наиболее широко применяемых систем исчисления в компьютерных науках является двоичная система исчисления. В двоичной системе используются только две цифры - 0 и 1. Эта система является основой для работы с компьютерными данными. Все данные, хранящиеся и обрабатываемые компьютерами, являются двоичными - состоят из нулей и единиц.
Двоичная система исчисления используется для представления и обработки чисел, текста, изображений и звука. Она позволяет компьютерам эффективно хранить и передавать информацию. Каждая цифра в двоичной системе имеет определенное значение, и их комбинации могут представлять как числа, так и другие типы данных.
Компьютерные программы и алгоритмы также используют систему исчисления для выполнения различных операций. Например, при выполнении арифметических операций компьютер преобразует числа в двоичной системе исчисления во время вычислений. Также используются другие системы исчисления, такие как восьмеричная и шестнадцатеричная системы исчисления, которые упрощают работу с большими числами.
Криптография - еще одна область компьютерных наук, где системы исчисления играют важную роль. Криптографические алгоритмы используют системы исчисления для шифрования и дешифрования информации. Например, шифр Цезаря использует алфавитную систему исчисления для сдвига букв в сообщении. Также используются другие системы исчисления, такие как шифр Виженера, шифр RSA и другие, которые обеспечивают безопасность передаваемой информации.
В компьютерных науках системы исчисления важны для понимания работы компьютеров, алгоритмов и программ. Они помогают разработчикам создавать эффективные алгоритмы, управлять данными и обеспечивать безопасность информации. Понимание систем исчисления является фундаментальным для работы в области компьютерных наук.
Вопрос-ответ
Какие существуют виды систем исчисления?
Существует несколько видов систем исчисления: двоичная, десятичная, шестнадцатеричная и др. Каждая из них основана на определенном числовом основании и используется для представления чисел в различных областях.
Что такое двоичная система исчисления?
Двоичная система исчисления - это система, основанная на двух символах: 0 и 1. Она широко используется в компьютерах и электронике для представления информации.
Каково применение шестнадцатеричной системы исчисления?
Шестнадцатеричная система исчисления используется в программировании и компьютерах для представления чисел и данных. Она позволяет удобно и компактно записывать большие числа и двоичные данные.
Какие примеры использования десятичной системы исчисления в повседневной жизни?
Десятичная система исчисления является основной системой для записи и работы с числами в повседневной жизни. Она используется при подсчете денег, измерении времени, рассчете расстояний и многих других областях.
В каких областях применяется система исчисления с основанием 64?
Система исчисления с основанием 64 применяется в некоторых компьютерных системах и сетях для представления больших объемов данных. Она также используется в некоторых алгоритмах шифрования и сжатия информации.